Abstract elementary class

In model theory, an abstract elementary class, or AEC for short, is a class of models with a partial order similar to the relation of a substructure of an elementary class in first-order model theory. They were studied by Shelah (2009).

1 Definition
2 Examples
3 Shelah's Categoricity Conjecture
4 Results
5 References

Definition

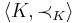$\langle K, \prec_K\rangle$ , for K a class of structures in some language L, is an AEC if it has the following properties:

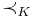$\prec_K$ is a partial order on K
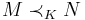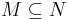
If $M\prec_K N$ then $M\subseteq N$
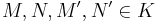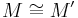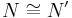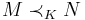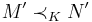
Isomorphisms: K is closed under isomorphisms, and if $M,N,M',N'\in K$ such that $M\cong M'$ , $N\cong N'$ , and $M\prec_K N$ then $M'\prec_K N'$
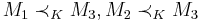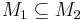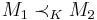
Coherence: If $M_1\prec_K M_3, M_2\prec_K M_3$ , and $M_1\subseteq M_2$ then $M_1\prec_K M_2$
Tarski-Vaught Chain Axioms If 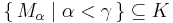is a chain, ie.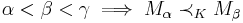
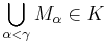
- $\bigcup_{\alpha<\gamma} M_\alpha\in K$
- if 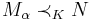$M_\alpha\prec_K N$ , for all 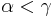$\alpha<\gamma$ , then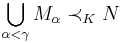 $\bigcup_{\alpha<\gamma} M_\alpha\prec_K N$
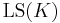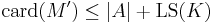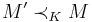
Löwenheim–Skolem Axiom There exists a cardinal denoted by $\operatorname{LS}(K)$ , such that if A is a subset of the universe of M, then there is M' in K whose universe contains A such that $\operatorname{card}(M')\leq |A|%2B\operatorname{LS}(K)$ and $M'\prec_K M$

Examples

Elementary classes are the most basic example of an AEC, when taken with $\prec$ taken to be elementary substructure.
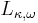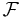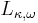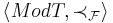If $\kappa$ is a cardinal, $T$ is a theory in the infinitary logic $L_{\kappa, \omega}$ , and $\mathcal{F}$ is a fragment of the $L_{\kappa, \omega}$ containing $T$ , then $\langle Mod T, \prec_{\mathcal{F}} \rangle$ is an AEC.

Shelah's Categoricity Conjecture

The work done on AECs is in large part done to prove Shelah's categoricity conjecture, which is a conjecture analogous to Morley's categoricity theorem in first-order model theory.

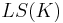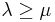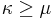The conjecture states, in simple terms, for every AEC K there is some cardinal $\mu$ (which depends only on $LS(K)$ ) such that if K is categorical at some $\lambda\geq\mu$ , ie. every model of size $\lambda$ is isomorphic, then K is categorical at all $\kappa\geq\mu$ .

Results

The following are some important results about AECs:

Shelah's Presentation Theorem: Any AEC 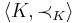$\langle K,\prec_K\rangle$ can be written as a PC class, where the language is of size 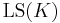$\operatorname{LS}(K)$ and we omit at most 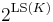$2^{\operatorname{LS}(K)}$ many types.

References

Shelah, Saharon (2009), Classification theory for elementary abstract classes, Studies in Logic (London), 18, College Publications, London, ISBN 978-1-904987-71-0
Shelah, Saharon (2009), Classification theory for abstract elementary classes. Vol. 2, Studies in Logic (London), 20, College Publications, London, ISBN 978-1-904987-72-7